In 1913, Danish Scientist Neils Bohr proposed a model of the atom which was based upon the Planck's quantum theory of radiation. The basic postulates of Bohr's theory are:
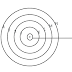
• An atom consists of a small heavy positively charged nucleus in the centre surrounded by electron. The electron in an atom revolve around the nucleus only in certain selected circular paths, called orbits. these orbits are associated with definite energies and are called shells or energy levels. These are numbered as 1,2,3,4...........etc. orbits or designated as K,L,M,N............etc. shells.
 |
| Fig: Bohr's orbits in an atom |
• As long as electron remains in a particular orbit, it dos not lose or gain energy. This means that the enery of the electron in a particular energy level remains constant. Therefore, these circular orbits are called stationary states. The term stationary does not mean the electron is stationary but it means that the enery of the electorn does not change with time. This accounts for the stability of an atom.
• Only those orbits are permitted in which the angular momentum of the electron is a whole number multiple of h/2π (where h is planck's constant). The electron, like any other moving body, moving in a circular orbit has an angular momentum is equal to mνr. According to Bohr,
mνr = nh/2π
m = mass of electron
r = radious of an atom
ν = velocity
n = 1,2,3...............
This postulates, therefore, introduces the concept of quantization of angular momentum.
• When energy is supplied to an atom, its electrons absorb energy and jump to higher enery level. As soon as supplied source of energy is cut, electron jumps back to the original level. A transition from one stationary state to another is accompanied by emission or absorpation of energy equal to the difference between in energy of two state. If E1 is the energy in state 1 and E2 is the energy in state 2, then change of energy E2-E1 in electron jump is given by
ν = E2-E1/h
where ν is the frequency of the emitted radiations and h is Planck's constant.




0 Comments